Permutations are a key topic in quantitative aptitude, testing your understanding of arrangement, order, and logical reasoning. From exam halls to interviews and placements, permutation-based questions often serve as a filter for evaluating analytical thinking under constraints.
What is a Permutation?
Permutation is the arrangement of items in a specific order.
- If you’re choosing r elements from a set of n distinct elements:
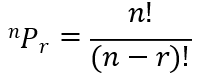
- If all elements are arranged (r = n), it becomes n!
Six Common Types of Permutation Questions
1. Simple Arrangements
These involve choosing and arranging r items out of n distinct elements.
Q: In how many ways can 4 people be selected and arranged from a group of 6?
Solution: We are selecting and arranging 4 out of 6 people:
6𝑃4 = 6 ⋅ 5 ⋅ 4 ⋅ 3 = 360
2. Word Formation Problems
These questions ask for the number of ways to rearrange the letters of a word, considering repeated letters (if any).
Example:
Q: How many distinct words can be formed using the letters of the word “APPLE”?
Solution: “APPLE” has 5 letters, with P repeated twice.
Number of words = 5!/2! = 120/2 = 60
3. Restricted Position Questions
These involve constraints like starting/ending digits or specific placements.
Example:
Q: How many 4-digit numbers can be formed using digits 1 to 9 without repetition?
Solution:
- First digit (thousands place): 1–9 → 9 options
- Remaining: choose 3 from the remaining 8 digits → 8𝑃3
= 9 ⋅ 8 ⋅ 7 ⋅ 6 = 3024
4. Permutations with Identical Objects
When some objects are indistinguishable, divide by the factorials of identical items.
Example:
Q: How many arrangements of the word “BALLOON” are possible?
Solution: “BALLOON” has 7 letters with:
- L repeated twice
- O repeated twice
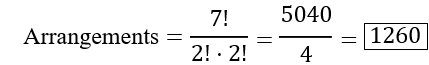
5. Circular Permutations
In circular arrangements, one object is fixed and the rest are arranged around it.
Example:
Q: In how many ways can 5 friends sit around a round table?
Solution: In circular permutations:
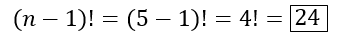
6. Conditional Permutations (Objects Together or Apart)
Here, certain elements must always or never be together.
Example:
Q: In how many ways can 6 books be arranged on a shelf if 2 particular books must be together?
Solution:
- Treat 2 books as 1 unit → total units = 5
- Arrangements = 5! ⋅ 2! = 120 ⋅ 2 = 240
(2! accounts for internal arrangement of the grouped books)
Test-Taking Strategies for Permutation Questions
1. Use the Slot Method for Clarity
Draw blank spaces for each position and fill in possibilities.
Helps especially in digit or letter arrangements with restrictions.
Identify:
- Are items distinct?
- Are there repetitions?
- Are there restrictions?
- Is the arrangement circular?
Break the problem into selection + arrangement.
3. Don’t Confuse Permutations with Combinations
In permutations: Order matters; In combinations: Order doesn’t matter
“ABC” and “CAB” are different permutations, but the same combination.
4. Memorize Key Factorials and Formulas
At least up to 7!:
- 3! = 6, 4! = 24, 5! = 120, 6! = 720, 7! = 5040
5. Apply the Complement Rule in ‘Not Together’ Problems
When elements must not be together:
Total permutations − Permutations where they are together
Common Pitfalls to Avoid
- Forgetting to handle repetitions (especially in word problems)
- Treating circular arrangements like linear ones
- Including 0 as first digit of a number
- Misidentifying when objects are identical or distinct
- Confusing permutation with combination
Mastering permutations requires a mix of conceptual clarity and pattern recognition. With structured problem-solving, attention to detail, and ample practice, you’ll be well-prepared to handle any permutation problem that comes your way on aptitude tests.
For practice, log on to:









